Bad numbers in the "gzip beats BERT" paper?

Published 2023 / 07 / 17

For updates: See the github issue and the follow-up blog post.

The recent paper,“Low-Resource” Text Classification: A Parameter-Free Classification Method with Compressors by Jiang et al. [link] recently received a lot of attention on twitter.

I recently checked out their source code to try to recreate their results and to try out some related ideas.

What I found is that their kNN classifier code is using a non-standard method of computing accuracy to be a bug (or at least an unexpected choice) in their kNN code that makes all the accuracy numbers for their method higher than expected. [tldr: it is reporting something like top-2 accuracy rather than a normal kNN(k=2) accuracy].

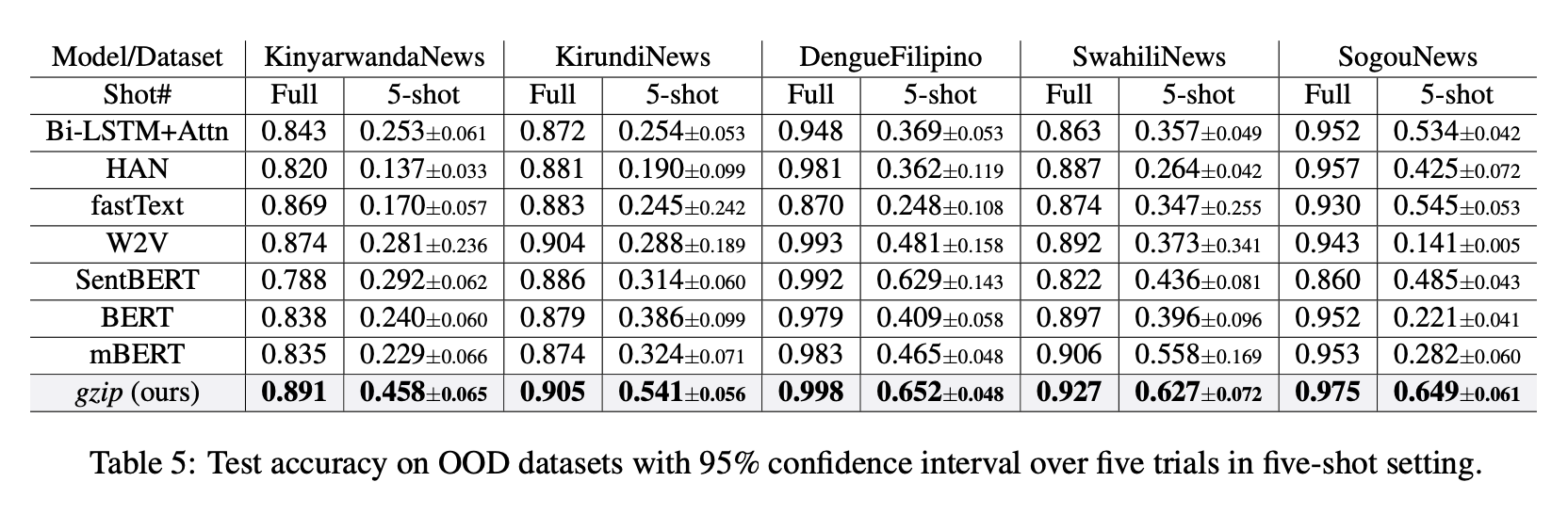
Table 5 from the paper was often included in tweets and shows the gzip method beating all these other neural-network-based methods:

I'll explain the details below, but my calculations for these experiments are (first 4 datasets, only the "Full" column):

	KinyarwandaNews	KirundiNews	DengueFilipino	SwahiliNews
in paper	0.891	0.905	0.998	0.927
corrected (knn2d)	0.835	0.858	0.999	0.850

(Fifth dataset SogouNews is large -- I haven't run it yet)

These numbers would significantly change the take-away from these experiments. For example, for KirundiNews, the gzip method went from best-perfoming to worst-performing.

kNN

Their method uses a kNN classifier using k=2 (Appendix C says all experiments used k=2).

k=2 is a bit of an odd choice for kNN classification. For every test case, you search the training set for the two "closest" examples. Looking at the labels of these two, there are only two possibilities,

The labels are equal. So, this is clearly your hypothesized label. Note that you would get the same answer for k=1.
The labels are different. We have a 1-1 tie that most be broken. There are many ways to do a tie breaker, but one reasonable one is take the label of the closer point. In this case, you get the same answer for k=1.

So, going from k=1 to k=2 doesn't add much information to your classifier. If you break ties with a random decision, then for 50% of the 1-1 ties you are choosing the further point, which is unlikely to improve over k=1.

It is in the case of ties that the source code here is doing something unexpected, shown below.

Code

The issue is in calc_acc method in experiments.py [here].

Here is the relevant snippet, with my added comments, and branches dealing with rand==True removed for clarity:

# here, sorted_pred_lab[][] has the 
# labels and counts corresponding
# to the top-k samples,
#  [[label,count],[label,count],...]
# grouped-by label and sorted by count.

most_label = sorted_pred_lab[0][0]
most_count = sorted_pred_lab[0][1]

if_right = 0
for pair in sorted_pred_lab:
    # we loop until we drop below 'most_count', ie
    # this for-loop iterates over those classes
    # tied for highest count
    if pair[1] < most_count:
        break

    # this says if ANY of those
    # in the tied-set are equal to
    # the test label,
    # it is marked correct (if_right=1)
    if pair[0] == label[i]:
        if_right = 1
        most_label = pair[0]

# accumulate results:        
pred.append(most_label)
correct.append(if_right)

So, if any of the tie-break labels is equal to the test label, it is marked as correct. For k=2, a tie simply means there was one vote for each of two different classes amongst the 2 closest training points. Therefore, the reported accuracies could be considered top-2, meaning that it's marked correct if either of the top two choices is correct (you may have encountered top-k in ImageNet, where top-5 accuracy is often cited). However, note that this concept of top-k is a bit different than normal usage because we are talking about k selected training points, rather than k selected labels.

This method takes arbitrary k but note that it doesn't compute top-k for any k. Only in the special case of k=2 do we have that when there is a tie, all the k examples are tied with the max value (1).

The calc_acc method has a rand flag that seems to be correct: if rand==True it will correctly break the tie using random.choice. But it seems that this wasn't used for the paper results.

Re-implementation

I wrote a simple implementation with two different tie-breaking strategies:

[r] random selection
[d] decrement k until you are left with a case without ties.

Results        
           kinnews  kirnews  filipino swahili 
table5     0.891    0.905    0.998    0.927   value in paper
code       0.891    0.906    1.000    0.927   using npc_gzip repo
top2       0.891    0.906    1.000    0.927   top-2
knn1r      0.835    0.858    0.999    0.850   kNN,k=1,tie=random
knn1d      0.835    0.858    0.999    0.850   kNN,k=1,tie=decrement
knn2r      0.828    0.807    0.851    0.842   kNN,k=2,tie=random
knn3r      0.838    0.791    0.851    0.881   kNN,k=3,tie=random
knn2d      0.835    0.858    0.999    0.850   kNN,k=2,tie=decrement
knn3d      0.843    0.794    0.904    0.883   kNN,k=3,tie=decrement

Update: My newer re-implementation has more complete results with many different k.

Some sanity checks:

table5 very close to code (within 0.001 or 0.002): able to recreate numbers from paper
code always equals top2. So the official code gives identical results to my completely separate implementation of top-2
knn1r == knn1d. There are never ties for k=1
knn2d == knn1d. For k=2, ties go to first, so same as using k=1.
knn2r < knn2d. For k=2, on a 1-1 tie, random is just taking the further one 50% of the time. So, it makes sence that's worse than just taking the closest.

todo:

Why is filipino so high (1.0 in one case)? Update: See my Part 2 that looks at problems with this dataset.
Why is 'table5' slightly different than 'code' in two cases?